Compare las siguientes respuestas a la pregunta ¿dónde puede Ud. disfrutar de la exposición Laberintos Coordenados?
¿Cuál de las descripciones es más breve y precisa? Imagino que el lector estará de acuerdo en que dos números son una representación mucho más concisa de un lugar que una larga descripción. Pero ¿qué significan esos números? ¿cómo han de interpretarse? ¿cuántas formas existen para asociar números a posiciones en el espacio? Éstas son algunas de las preguntas que se pretende contestar en esta exposición, la cual conjuga matemáticas, arte y juego.
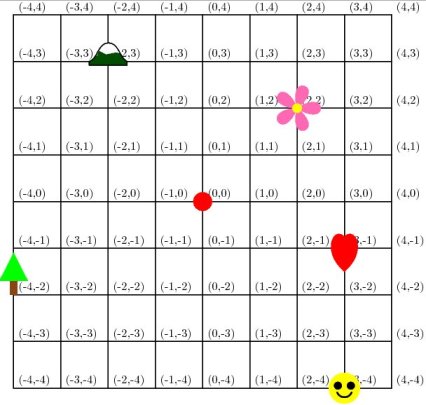
Una parte de la exposición mencionada arriba consiste de una serie de carteles que explican el concepto de coordenadas. Por ejemplo, la figura 1 nos muestra cómo podemos identificar los puntos de un plano con parejas de números de la forma (x,y). Así, la flor en la figura ocuparía el punto con coordenadas (2,2) pues podemos llegar a ella dando dos pasos hacia la derecha y dos hacia arriba a partir del origen señalado con un punto rojo. De la misma manera, el árbol ocuparía el punto con coordenadas (-4,-2), pues para llegar a él hay que caminar cuatro pasos a la izquierda y dos para abajo, o equivalentemente, -4 pasos hacia la derecha y -2 pasos hacia abajo.
 |
Figura 1: Coordenadas rectangulares. Habiendo escogido un origen (punto rojo), un par de orientaciones ortogonales (líneas horizontales y verticales) y una unidad de medición (tamaño de cada cuadrito), cada punto de un plano puede describirse mediante un par de números de la forma (x,y), donde x denota cuántos pasos deben darse hacia la derecha y y cuántos hacia arriba para llegar desde el origen hasta el punto en cuestión. |
Así como un sistema coordenado permite identificar puntos en el plano con pares coordenados, Descartes mostró en el siglo XVII que el mismo sistema coordenado permite identificar ecuaciones con figuras geométricas, unificando así el estudio matemático del álgebra con el de la geometría. Actualmente, las coordenadas se emplean en todas las áreas de la ciencia y la tecnología. Por ejemplo, todos las fotografías digitales y los dibujos generados por computadora se describen en términos de coordenadas.
 |
Figura 2: Los dibujos en computadora se describen en términos de coordenadas cartesianas. Por ejemplo, el cuerpo y la cola de uno de los pescaditos de esta figura es la línea que interpola los puntos (-3,0), (-4,-1), (-2,0), (-1,0.5), (0,1), (1,1), (2,0), (1,-1), (0,-1), (-1,-0.5), (-2,0), (-4,1), (-3,0), algunos de los cuales están indicados con puntos rojos. Las aletas corresponden a los puntos (-1,.5), (-1,2), (1,1) y (-1,-.5), (-1,-2), (1,-1), la boca a (1,0),(2,0) y el ojo a (1,0.5) |
Una vez entendido el concepto de coordenada es natural hacernos la pregunta ¿cuántas coordenadas necesitamos? Se ilustran entonces en la exposición distintos espacios cuya descripción requiere de distintas cantidades de coordenadas, es decir, con diferentes números de dimensiones. Además de las líneas rectas o curvas con una dimensión, superficies planas o curvas con dos y volúmenes tres dimensiones, hay otros sistemas con más dimensiones, como el espacio-tiempo de cuatro dimensiones, la postura del cuerpo humano con decenas de dimensiones, el espacio de posibles acordes musicales, de alrededor de un centenar de dimensiones y el espacio de configuración de un gas con millones de millones de millones de millones de dimensiones. Y hay espacios con aún más dimensiones. Si bien el conjunto de todas las sensaciones que pueden producir los colores en nuestros ojos puede describirse como un espacio de tres dimensiones, el espacio de todos los colores posibles es de infinitas dimensiones, así como el espacio de todos los posibles timbres musicales.
Además de existir muchos espacios, cada uno de ellos puede describirse en términos de muchos sistemas coordenados distintos. Así, adicionalmente a las coordenadas cartesianas, en la exposición se ilustran las coordenadas logarítmicas, oblicuas (figura 3), polares, elípticas (figura 4) y bi-angulares (figura 5), entre otras.
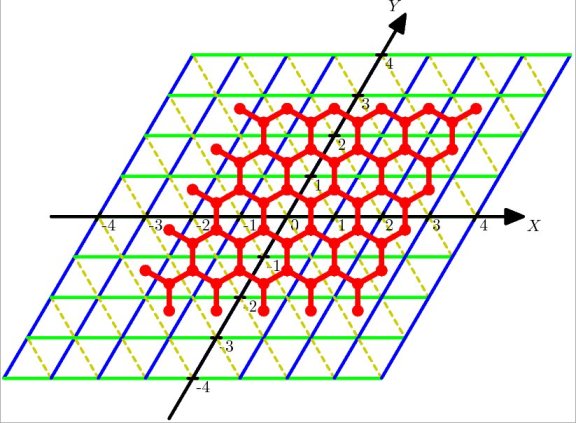 |
Figura 3: Coordenadas oblicuas. Algunos sistemas, como los cristales, se describen más fácilmente empleando sistemas coordenados formados por familias de rectas que no necesariamente son perpendiculares entre sí sino oblicuas. Por ejemplo, el grafeno es un cristal bidimensional que es mejor descrito en un sistema coordenado formado por paralelogramos formados cada uno por dos triángulos equiláteros. |
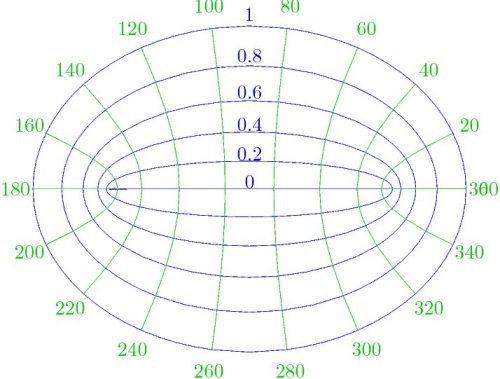 |
Figura 4: Algunas ecuaciones de la física matemática se simplifican en sistemas coordenados formados por retículas de líneas que no son rectas, como las coordenadas elípticas formadas por familias de elipses y de hipérbolas. |
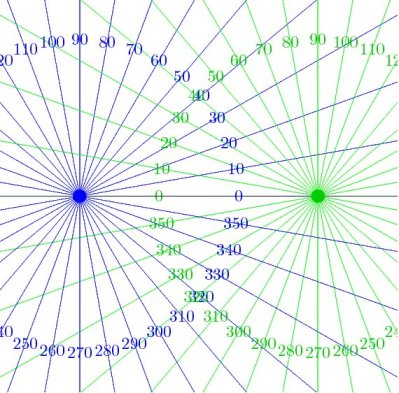 |
Figura 5: Las coordenadas biangulares están formadas por dos familias de rectas que irradian desde dos puntos distintos. Cada recta está caracterizada por un ángulo, de manera que cada punto del plano está caracterizado por dos ángulos. |
Las coordenadas bi-angulares consisten de dos ángulos correspondientes a las direcciones a las que tenemos que voltear para ver un objeto desde dos puntos de vista distintos. Cuando los dos puntos de vista corresponden a nuestros dos ojos, las coordenadas bi-angulares nos dicen en que dirección debemos voltear la vista para observar al objeto y nos dicen cuánto tenemos que hacer converger los ojos para que ambos apunten hacia el mismo objeto. Esta información es la que nos permite la estereoscopía, es decir, nos permite averiguar a qué distancia de nosotros se encuentra el objeto (figura 6).
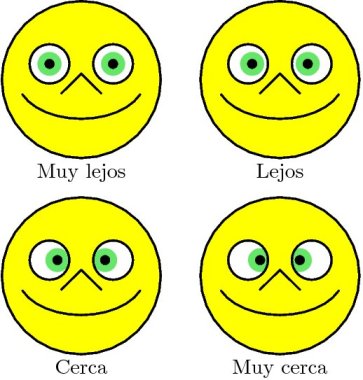 |
Figura 6: La estereoscopía nos permite determinar si un objeto se halla cerca o lejos de nosotros de acuerdo a la convergencia de nuestros ojos. Si el objeto está lejos, nuestros dos ojos apuntarán en direcciones paralelas. Si el objeto es cercano, tendremos que hacer bizcos haciendo converger nuestra vista sobre el objeto. La figura muestra una cara observando objetos que se hallan a distintas distancias. |
Otra parte de la exposición consiste de una obra artística dinámica que se anima de movimiento conforme el espectador camina enfrente de ella. La obra consiste de ondas que avanzan en distintas direcciones y discos que giran en distintos sentidos con distintas velocidades (figura 7).
 |
 |
 |
 |
| Figura 7: Algunas figuras formadas por ondas que avanzan y discos que giran cuando el observador camina enfrente de ellas | |
Podemos entender cómo se logra este movimiento si tomamos dos peines idénticos y los colocamos uno detrás del otro. Como ilustra la figura 8, además de los dientes de uno y otro peine, aparece una serie de líneas que no pertenece ni a uno ni a otro sino que se forman por la superposición de ambos. El patrón de líneas que emerge al superponer los peines, así como el que emerge al superponer dos telas de mosquitero y o cualesquiera dos sistemas con una textura que se repite casi periódicamente, se conoce como patrón de moiré. Un pequeño movimiento o giro de uno de los peines con respecto al otro produce un movimiento grande del patrón de moiré, como el lector podría verificar fácilmente.
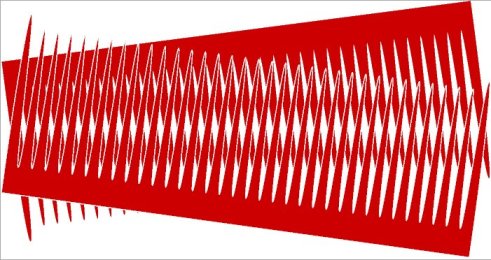 |
Figura 8: Al colocar dos peines idénticos, uno detrás del otro, aparecen una serie de líneas obscuras y claras (líneas horizontales en la figura) que no pertenecen a uno ni a otro peine, sino que se forman debido al efecto moiré. |
En la exposición se presenta una explicación del efecto moiré y de la técnica matemática que fue desarrollada en el Instituto de Ciencias Físicas de la UNAM para aprovecharlo y sintetizar imágenes que se mueven de manera prescrita conforme camina el observador. Acuñamos el nombre de codificación y detección homodina (en fase) de imágenes en movimiento por su similitud a otra técnica de nombre similar empleada en el pasado para codificar señales de audio en ondas de radio y posteriormente detectarlas para producir sonido.
Además, aprovechando el que cada imagen se ve diferente desde distintos puntos de vista, es decir, desde distintas orientaciones, pudimos codificar distintos puntos dentro de la sala de exposiciones en términos de parejas de imágenes que forman una contra-parte gráfica de las coordenadas bi-angulares correspondientes. Mediante secuencias de pares de imágenes formamos caminos ocultos en la sala, laberintos que el visitante debe descubrir e identificar para escapar de ellos. Estos laberintos fueron presentados por primera ocasión en el Museo Universitario de Arte Contemporáneo de la UNAM en agosto de 2010. Las imágenes en movimiento se han presentado en el Museo de la Luz, Universum, Museo de los Metales, Museo de Ciencias de Morelos, en institutos universitarios, en plazas públicas y en el metro de la ciudad de México.
El carácter lúdico de la exposición queda complementado con una grandes tableros de juegos relacionados con coordenadas, como son batalla naval, gato tri-dimensional y cinco en línea.
La exposición Laberintos Coordenadas fue preparada por Roberto Jiménez Álvarez, Ana Libia Marín Silva y Pablo Padilla Longoria, además del autor de este artículo y contó con un fuerte apoyo del Museo de Ciencias de Cuernavaca y de su personal. Puede visitarse de las ... hasta las ... horas los siete días de la semana y permanecerá abierta desde el día ... hasta el día ...